Bernhard
Peter
Jantar
Mantar - astronomische Geräte Indiens, Teil 5:
Das Samrat Yantra in Jaipur
Das Samrat Yantra ist zweifellos das größte und augenfälligste der Instrumente in Jaipurs Jantar Mantar. Es wurde von Jai Singh selbst konstruiert und im Jahre 1724 AD erbaut. Im Wesentlichen ist es eine gigantische Sonnenuhr, deren Präzision vor allem durch die schiere Größe des Instrumentes erreicht werden soll. Ein kleineres Instrument gleicher Bauweise ist das Laghu Samrat Yantra, es ist nur ein Viertel so groß. Ein Instrument vom Typ des Samrat Yantra war in allen fünf Observatorien von Jai Singh aufgestellt.
Konstruktion des Instrumentes:
Hauptbau ist ein Gnomon, ein
Sonnenzeiger in Form einer dreieckigen Rampe, 44 m lang, 27 m
hoch, mit einer Treppe auf der Rampe, oben bekrönt von einem
zierlichen pavillonartigen Aufsatz (Chatri), dessen Leichtigkeit
ätherisch anmutet zu der markanten Schwere und Strenge des
Gnomons selbst. Dahinter fällt das Gnomon senkrecht ab (im
Gegensatz zum Laghu Samrat Yantra).
Die Treppe selbst ist beiderseits von einem Marmorband gesäumt.
Das Chatri ist ein typisches Element rajputischer Architektur,
wie auch an Palästen zu finden. Aber hier oben markiert es den
Punkt, an dem die vier Himmelsrichtungen und die Hauptrichtungen
des Universums kulminieren. Das Chatri wurde als
Beobachtungspunkt benutzt, z. B. für die Windrichtung,
Himmelsereignisse oder Wetter, z. B. Beginn des Monsuns etc. Auch
heute noch wird es für religiöse Zwecke benutzt. Das Gnomon ist
genau entlang der Nord-Süd-Achse ausgerichtet, mit dem hohen
Ende nach Norden. Zu beiden Seiten des Gnomons befinden sich zwei
Quadranten wie riesige marmorne Schwingen. Ein mit gravierten
Skalen für Stunden, Minuten und Sekunden versehenes Marmorband
schwingt sich auf den Unterbauten in elegantem Bogen von ca. 15 m
Durchmesser in die Höhe, parallel zum Erdäquator. Das Gnomon
hat zwischen den beiden Marmorskalen insgesamt drei Treppen, zwei
schmale jeweils an den Skalen entlang und eine breitere vertieft
in der Mitte.

Das Samrat Yantra hat an der Ostseite des Gnomons oben zwei steinerne Halterungen für einen Flaggenmast. Eine solche Fahne konnte dort angebracht werden, um die Windrichtung festzustellen, um das Wetter abzuschätzen, insbesondere an den Vollmondtagen vor Beginn der Regenzeit.
Was leistet das Samrat Yantra?
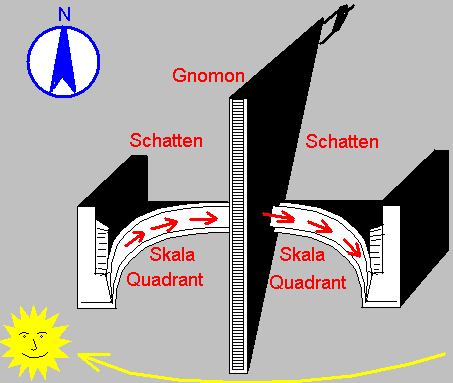
Der Hauptzweck war die
Bestimmung der Zeit nach dem Sonnenstand, also die Messung der
täglichen Sonnenbewegung (an den Quadrantenflügeln), und die
Messung der jährlichen Sonnenbewegung (entlang der Rampe bzw. an
den Shastansha Yantras im Innern der Seitentürme). Mit der
aufsteigenden Sonne erscheint der Schatten zuerst auf der linken
äußeren Seite der Skala des westlichen Quadranten, läuft dann
mit steigender Sonne an der Marmorskala entlang herab, taucht
schließlich zur Mittagszeit unter dem Gnomon durch (kein
Schatten zu sehen) und läuft an der östlichen Skala wieder
hinauf, bis die Sonne am westlichen Horizont versinkt. Die
Quadrantenskalen erlauben das Ablesen der Uhrzeit und auch der
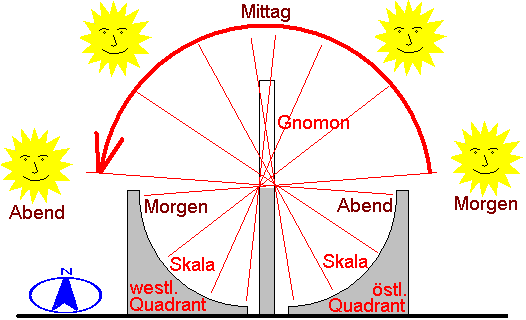
Länge des Tages. Die Skalen sind in Form eines weiten
Kreissegmentes gebogen und im Raum schräggestellt, damit sie
parallel zum Erdäquator sind, damit zu jeder Tageszeit ein
möglichst waagerechter Strich auf der Skala erreicht wird.
Deshalb ist die Skala für die späten Vormittags- und frühen
Nachmittagsstunden relativ flach, die für die frühen Morgen-
und späten Abendstunden (flache Sonne) aber relativ steil und
schräg. Aufgrund der Eigenbreite des Gnomons kommt eine weitere
Eigenart ins Spiel: Vormittags ist die westliche Außenkante des
Gnomons maßgeblich, nachmittags die östliche Außenkante. Die
Skala ist damit per se diskontinuierlich, was aber der
Genauigkeit keinen Abbruch tut. Auf der Westskala laufen die
Markierungen von 6 in 1-Stunden-Abständen bis 12, auf der
Ostskala von 12 bis 6. Ein Abschnitt einer Stunde ist erst in 2
Abschnitte zu je 1/2 h, dann weiter in je 30 Abschnitte zu je 1
Min, dann weiter in je 10 Abschnitte zu je 6 sec und zuletzt noch
einmal in je 3 Abschnitte zu je 2 sec eingeteilt. Aufgrund der
enormen Größe sollte die Sonnenuhr prinzipiell relativ genau
sein. 1 Stunde entspricht ca. 4 m auf der Skala, 1 Minute ca. 6.7
cm, 2 Sekunden ca. 2 mm. Die Skalen sind jeweils am nördlichen
und am südlichen Rand der Marmorflächen aufgetragen.
Sekundäre Funktionen sind Bestimmung des Ortes des Polarsternes und Beobachtung der Wege der Sterne am Himmel.
Die Rampe ist so gebaut, daß die Schräge genau parallel zur Erdachse steht. Jaipur liegt auf 27° geographischer Breite (genauer: Jaipur liegt auf 26°55'27'' Nord und 75°49'18.8'' Ost), folglich weicht der örtliche Horizont um ca. 27° von der Erdachse ab. Die Rampe (Hypotenuse des Dreiecks) korrigiert dieses wieder. Damit liegt die Rampe parallel zur Erdachse und deswegen weist der Blick entlang der Rampe direkt auf den Polarstern. Wenn dem nicht so wäre, würde der Schatten des Gnomons zu einer Vergleichsstunde zu verschiedenen Jahreszeiten in verschiedene Richtungen seinen Schatten werfen. Außerdem würde der Winkel, der in einer gegebenen Zeit durchschritten wird, ebenfalls von den Jahreszeiten abhängig sein. Die Parallelität von Gnomon und Erdachse ist damit eine fundamentale Voraussetzung für richtig gehende Sonnenuhren.
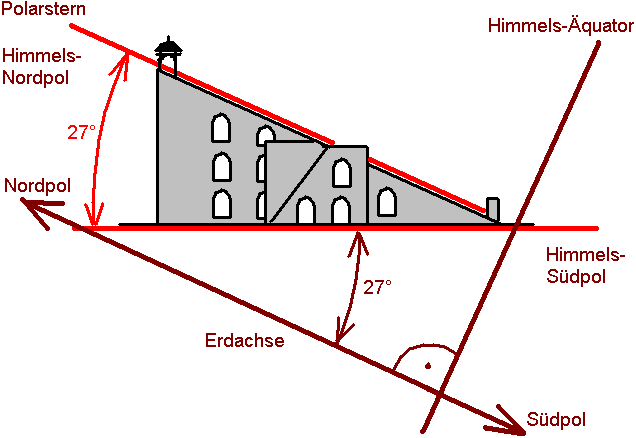
Hier wird alles aus der Perspektive des auf der Erdoberfläche Stehenden und Wahrnehmenden beschrieben.
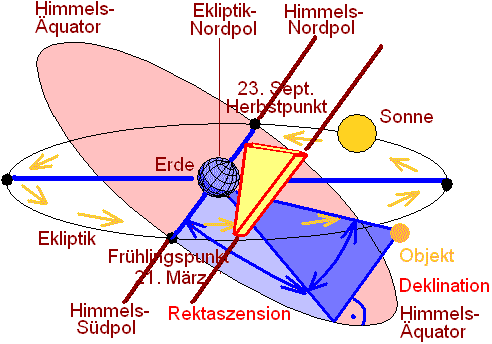
Über die Skala an der Rampe können wichtige Punkte im Jahr bestimmt werden. Denn die Sonnenbahn wird im Frühjahr immer steiler, erreicht ihren höchsten Punkt am Himmel zur Sommersonnenwende, und wird dann immer flacher, bis sie ihren tiefsten Punkt zur Wintersonnenwende erreicht. Die flügelartigen Skalen sind fest in Relation zur Rampe. Wenn die Sonnenbahn höher ist, wird ein anderer Abschnitt der Rampe auf die Skalen projiziert als im Winter, wo ein unterer Abschnitt projiziert wird. Durch Beobachtung der Projektionslinien und entsprechender Skalierung kann so an der Rampe ein Jahreskalender der Sonne abgelesen werden und können so die Sonnenwenden sowie die Tagundnachtgleichen bestimmt werden. Entsprechende Markierungen an der Rampe korrespondieren mit Linien auf den Quadrantenflügeln. Viel besser geht das natürlich mit dem Shastansha Yantra im Inneren der Seitentürme.
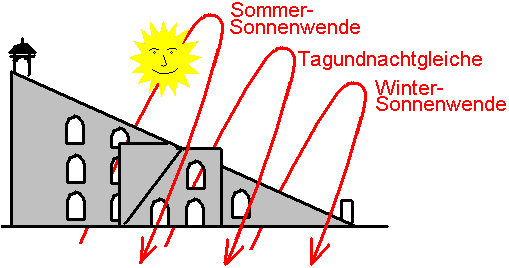
Die Hypothenuse ist ebenfalls mit Skalen versehen, sowohl auf der rechten Kante als auch auf der linken Kante, einmal für die Vormittagsbebachtung, einmal für die Nachmittagsbeobachtung. Im Detail ist das noch ein bißchen komplexer: Auf jeder Seite sind genau zwei Skalen angebracht, eine beginnend oberhalb der Mitte und zum flachen Ende des Gnomons laufend, die andere unterhalb der Mitte beginnend und zum oberen (hohen) Ende des Gnomons laufend. In der Mitte des Gnomons gibt es eine Zone, wo sich beide Skalen überlappen, in diesem Bereich springt eine Skala nach innen und wird parallel in der Überlappungszone weitergeführt. Welchen Sinn macht das? Mit diesen Skalen kann man die Deklination der Sonne bestimmen. Der Schatten auf den Quadrantenskalen sieht immer gleich aus, unabhängig davon, welcher Teil der Kante ihn im Lauf eines Jahres wirft. Um festzustellen, welcher Teil der Kante den Schatten wirft, positioniert man an der Kante senkrecht zu dieser einen kurzen Schattenstab. Wenn er senkrecht zur Rampe steht, ist der Schatten genau parallel zur Kante des Quadranten. Man bewegt den Schattenstab nun an der Kante entlang, bis er genau an der Kante der Quadrantenfläche liegt- dann kann man an der Hypotenusen-Skala die Deklination der Sonne ablesen. Und in der einen Jahreshälfte nimmt man die eine Quadrantenskala und die nach oben laufende Hypotenusen-Skala, in der anderen Hälfte die andere Quadrantenskala und die nach unten laufende Hypotenusen-Skala. Soweit zur Sonne.
Mit Hilfe von Peilungen von der Quadrantenskala entlang der Rampenskala kann man auch beliebige andere Himmelskörper (Sterne, Planeten) anvisieren. An den Peilpunkten kann man jeweils die Positionsdaten ablesen. Was das Samrat Yantra nicht leistet, ist eine Sternbeobachtung mit Peilschnüren oder langen Peilstäben von Skala zu Skala, das ist praktisch nicht realisierbar wegen der großen Dimensionen: Ein Peilstab wäre zu groß zum Hantieren, außerdem würde er sich bei der zu überbrückenden Distanz durchbiegen, eine Schnur würde man ebenfalls auf diese Distanz nicht gerade spannen können, sie würde immer im Sinne einer Catena-Funktion durchhängen, und jeder Versuch, sie gerade zu spannen, würde zum Reißen führen. Das Anpeilen von Sternen geht nur folgendermaßen: Ein Beobachter steigt an der Quadrantenkante entlang, bis der Stern des Interesses genau über der Gnomonkante steht, er also die richtige Rektaszension gefunden hat. Ein Helfer läuft mit einem kleinen Stab die Treppe des Gnomons entlang und positioniert diesen solange neu, bis der Beobachter ihn in Linie mit dem Stern sieht. Die Verwendung einer Blendlaterne könnte hilfreich sein. Nun kann der Helfer die Deklination ablesen. Hier ist wichtig, daß die Rampe genau parallel zur Erdachse verläuft und auf den Polarstern ausgerichtet ist, das System also auf Erdachse und Äquator basiert: Man erhält äquatoriale Koordinaten, nämlich Rektaszension (seitliche Abweichung) und Deklination (Höhenabweichung).
Was leistet das Samrat Yantra nicht?
Schlimm für die Genauigkeit
des Systems wirkt sich ein systematischer Fehler aus: Die Sonne
wirft aufgrund der eigenen Ausdehnung (30 Bogenminuten) einen
Kernschatten, der am Rand von einem Halbschatten begleitet ist,
der im Falle des Samrat Yantra 10 cm breit ist, also eine
Ungenauigkeit von 1.5 Minuten ins Spiel bringt! Der Schatten ist
nicht scharf definiert (Schattendiffraktion), der Übergang in
der Halbschattenzone ist ein Kontinuum. Je größer eine
Sonnenuhr ist, desto größer wird dieses Problem, und das Samrat
Yantra ist aufgrund seiner Dimensionen sehr anfällig für dieses
Problem. Besonders fällt das zur Mittagszeit auf. Rein
theoretisch verschwindet die Schattenlinie an der westlichen
Seite des Gnomons und taucht sofort danach als neuer Strich auf
der östlichen Seite des Gnomons wieder auf. Tatsächlich aber
braucht der Schatten ca. 80 Sekunden, um sich sichtbar von der
Mauer abzulösen. Wäre die Sonnenuhr kleiner gebaut, würde sie
nicht darunter zu leiden haben.
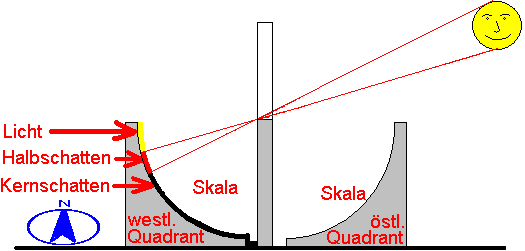
Der Vorschlag, das Problem durch die Verwendung von Schattenstäben, die man an die Rampe (Gnomon) hielt, und die Behauptung, daß damit die Uhr wieder genau im Sekundenbereich ginge, ist bei näherem Hinsehen nicht haltbar, weil sie ebenfalls unscharf abgebildet werden, und sehr dünne Gegenstände werfen über diese Distanz aufgrund der Schattendiffraktion überhaupt keinen Schatten auf dem Quadranten, wie die Praxis zeigt.
Die Schattendiffraktion austricksen!
Es gibt aber doch eine
Möglichkeit (Herrn Dr. Wedekind ein Dankeschön für den
Hinweis), die Schattendiffraktion auszutricksen: Der
schattenwerfende Gegenstand (Stäbchen, Streichholz, Stift o.ä.)
wird nicht an die Rampe gehalten, wo sein Schatten "verloren
ginge", sondern mit geringem Abstand (ca. 5 cm) über die
Skala am Quadranten selbst. Auf dem diffus verbreiterten Schatten
ist damit ein scharfer Schatten zu sehen, der natürlich in die
gleiche Richtung geworfen wird wie der Schatten des großen
Gnomons. Der Gegenstand wird nun über den unscharfen Bereich
bewegt. Dabei nimmt das Auge die Helligkeitsunterschiede zwischen
scharfem Schatten und diffusem Schatten wahr. Das Auge kann zwar
keine absoluten Helligkeiten detektieren, aber
Helligkeitsunterschiede sehr wohl. Wo beide Schatten gleich
dunkel sind, befindet sich der Übergang zwischen Kernschatten
und Halbschatten, der durch diesen Trick mit relativ großer
Genauigkeit bestimmt werden kann. Damit kann die Lage der Grenze
zwischen Kernschatten und Halbschatten wieder im Sekundenbereich
gemessen werden.
Ortszeit und indische Standardzeit
Die Sonnenuhr gibt Ortszeit
an, die für Jaipur gilt und der indischen Standardzeit
hinterherhinkt. Um auf indische Standardzeit zu kommen, muß man
bestimmte Korrekturwerte addieren:
| Monat/Tag | 5. | 10. | 15. | 20. | 25. | 30. |
| Januar | 32,10 | 34,18 | 36,13 | 37,50 | 39,09 | 40,08 |
| Februar | 40,52 | 41,06 | 41,06 | 40,38 | 39,58 | --- |
| März | 38,26 | 37,15 | 35,52 | 34,15 | 32,55 | 31,06 |
| April | 29,37 | 28,40 | 26,56 | 25,48 | 28,48 | 24,02 |
| Mai | 23,28 | 23,44 | 23,05 | 23,15 | 23,37 | 24,21 |
| Juni | 25,08 | 25,00 | 26,48 | 28,12 | 29,16 | 30,18 |
| Juli | 31,15 | 32,05 | 32,29 | 33,03 | 33,14 | 33,08 |
| August | 32,46 | 32,08 | 31,17 | 30,12 | 28,15 | 27,10 |
| September | 23,34 | 23,52 | 22,05 | 20,18 | 18,34 | 16,48 |
| Oktober | 15,18 | 13,54 | 12,39 | 11,38 | 10,56 | 10,28 |
| November | 10,25 | 10,43 | 11,22 | 12,24 | 13,44 | 15,24 |
| Dezember | 17,20 | 19,18 | 21,48 | 24,18 | 26,39 | 29,44 |
Photos, mehr Photos, Nächstes Kapitel, Zurück zur
Übersicht, Literatur
zu indischer Astronomie
andere Essays
über indische Kultur
![]() Home
Home
©
Text, Graphik und Photos: Bernhard Peter 2005
Impressum