Bernhard Peter
Jantar Mantar - astronomische Geräte Indiens, Teil 6:
Die Rashi Valaya Yantras in Jaipur

Konstruktion des Instrumentes:
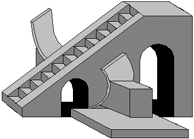
Im Aufbau ähnelt ein Rashi Valaya Yantra dem im vorigen Abschnitt beschriebenen Samrat Yantra. Der Bau besteht aus einer dreieckigen Rampe mit einer Treppe, die zu einer kleinen Plattform führt, die Treppe ist beiderseits von einer Zeigerkante gesäumt. Zu beiden Seiten der Rampe befinden sich zwei Quadranten wie marmorne Schwingen: Ein mit gravierten Skalen für Stunden, Minuten und Sekunden versehenes Marmorband schwingt sich auf den Unterbauten zu beiden Seiten im Bogen in die Höhe, aber im Vergleich zum Samrat Yantra sind es eher kleine Stummelflügel, denn ihr Radius beträgt nur 1 bis 1.5 m.

Und doch gibt es Unterschiede:

• Es handelt sich nicht um ein Einzelbauwerk, sondern um eine Gruppe von 12 ähnlichen Einheiten, die auf einer Plattform errichtet sind, die den Horizont repräsentiert.
• Sie sind wesentlich kleiner als das Samrat Yantra und der kleine Pavillon fehlt.
• Die 12 Rampen sind in ihrer Steigung unterschiedlich.
• Die 12 Einheiten sind zwar so arrangiert, daß sie zusammen harmonisch aussehen, doch jedes einzelne Rashi Valaya Yantra weist in eine andere Richtung. Sie sind möglichst symmetrisch arrangiert, doch ganz konnte man sich nicht nach ästhetischen Gesichtspunkten richten, weil die im Rücken der Anlage befindliche Palastmauer das Gelände schräg schneidet. (Achtung, in der Literatur bisweilen fehlerhaft dargestellt)

Das Rashi Valaya Yantra ist vom Verständnis her das komplexeste Instrument, weil es auf für uns, die wir mit den Füßen auf der Erde stehen, veränderlich scheinenden Bezugspunkten beruht. Die damit erhaltenen Daten beziehen sich auf ein Koordinatensystem, das im Grunde absolut ist, aber für uns auf der Erde scheinbar ständig um uns herumtorkelt. Der Schlüsselpunkt des Verständnisses ist, ein rotierendes Koordinatensystem zu akzeptieren. Dann ist der Rest ganz einfach.

Wie funktioniert das Instrument und was leistet es?
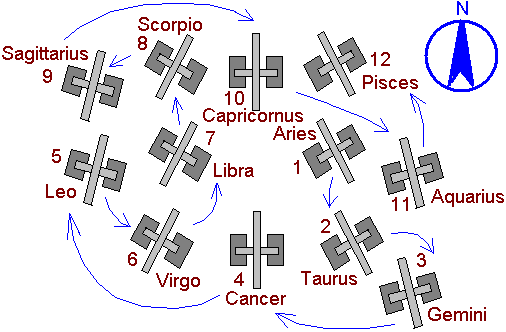
Es handelt sich um 12 Tierkreis-Gnomone - dieses Instrument orientiert sich an den 12 Tierkreiszeichen der Ekliptik. Zur Definition: Wenn man von der Erde aus die Position der Sonne auf die Himmelskugel projiziert, erhält man den Jahreskreis (Ekliptik). Er beschreibt den Weg der Sonne in Relation zu den Fixsternen, von der Erde aus betrachtet. Hier wird alles aus der Perspektive des auf der Erdoberfläche Stehenden und Wahrnehmenden beschrieben. 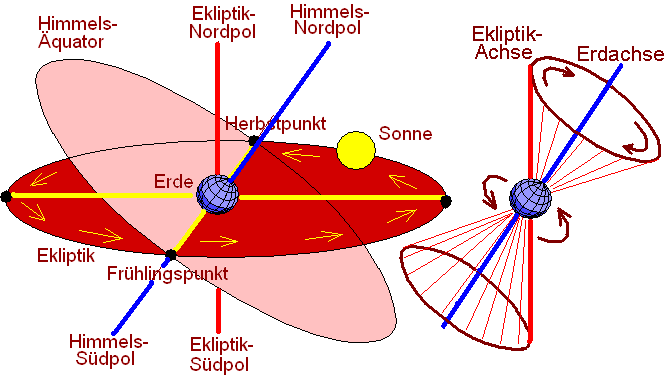Stellung von Jahreskreis und Himmelsäquator zueinander: Beide bilden einen Winkel von 23.5°, weil die Erdachse nicht senkrecht zur Umlaufbahn um die Sonne steht, sondern geneigt ist. Die Achse der Ekliptik steht senkrecht zur Ebene der Ekliptik, ihre Enden sind die Pole der Ekliptik. Wie die Erde im Laufe eines Tages um ihre schräggestellte Achse rotiert, so rotiert die Achse der Ekliptik um die Erdachse auf einer Art Kegelmantel.

Der Hauptzweck war die Bestimmung der Position der Sonne in Bezug auf die Tierkreiszeichen. Über die Funktionsweise der Quadrantenskalen gilt das beim Samrat Yantra Geschriebene analog, mit einem wichtigen Unterschied: Wir erhalten hier ekliptikale Koordinaten, d. h. die ekliptikale Länge und Breite der Himmelskörper, weil das Instrument anders ausgerichtet ist. Die ekliptikale Länge (Longitude) wird an den Quadrantenflügeln abgelesen, die ekliptikale Breite (Latitude) an den Skalen entlang des Gnomons. Die Beobachtung der Sonne ist trivial, weil ihre ekliptikale Breite immer Null ist, denn sie liegt definitionsgemäß in der Ekliptik. Die ekliptikale Länge der Sonne kann an den Quadrantenflügeln abgelesen werden. Aber in Bezug auf die Sonne und den Tierkreis kann die Position anderer Himmelskörper gemessen bzw. berechnet werden. Sterne kann man des Nachts mit einem Peilstab oder Peilrohr beobachten, das an die Skalen des Gnomons und des Quadranten angelegt wird.

Warum 12 Teilinstrumente?
Wir bräuchten also im Prinzip zur Messung von ekliptikalen Koordinaten ein bewegliches Instrument, dessen Achse jederzeit neu auf den Pol der Ekliptik ausgerichtet werden kann. Da das mit einem Bauwerk nicht geht, baute man einen Satz von mehreren Instrumenten mit jeweils fester Inklination und festem seitlichen Winkel, so daß immer wieder eines davon richtig steht.

Die Rampen sind so gebaut, daß zu bestimmten Beobachtungszeiten genau eine Rampe parallel zur Achse der Ekliptik ist, d. h. die Rampe ist in dem Moment auf den Pol der Ekliptik ausgerichtet. Da die Achse der Ekliptik um die Erdachse rotiert, verändert sich im Laufe eines Tages/Monats/Jahres ihre Lage ständig in Relation zur Erdachse und damit zur Beobachtungsebene, zur Bezugsebene, zur ebenen Plattform in Jaipur, auf der die Instrumente stehen. Die Lage der Ekliptikachse schwankt also theoretisch von 27°+ 23.5° = 50.5° bis 27° - 23.5° = 3.5°. Entsprechend weit gefächert ist auch die Neigung der Rampen. Es liefert immer nur ein Instrument von den 12 ein korrektes Ergebnis, sechsmal jeweils ein anderes am Tage, sechsmal eines der verbliebenen in der Nacht, weil nur eines die gerade richtige Rampenneigung hat. Dieses eine zeigt dann auf seinen Quadrantenflügeln ekliptikale Zeit bzw. ekliptikale Koordinaten an. Gemeinsam können alle 12 Instrumente die ekliptikalen Koordinaten eines ganzen siderischen Jahres abdecken und jeweils die richtige siderische Zeit angeben.

Wichtig zum Verständnis des Systems ist:

• Die Sonnenhöhe ist jahresabhängig.
• Und die Sonnenhöhe ist tageszeitabhängig
• Je nach Sonnenhöhe werden andere Teilinstrumente abgelesen
• Jeweils ein Instrument wird benutzt, wenn das betreffende Sternzeichen den lokalen Meridian erreicht, bzw. das betreffende Tierkreiszeichen auf dem lokalen Meridian kulminiert
• das richtige Teilinstrument ist das, bei dem die Sonne eine ekliptikale Breite von Null angezeigt bekommt, d. h. wo ein auf der Gnomonskala bei Null im rechten Winkel positionierter Schattenstab genau auf der Quadrantenkante abgebildet wird.
• Bei gleicher Tageszeit wechseln im Jahr die Instrumente im Monatsabstand durch
• Bei gleicher Jahreszeit wechseln im Tag die Instrumente im 2-Stunden-Abstand durch. Genau genommen ist nur alle 2 Stunden eine wirklich präzise Messung möglich, wie so viele andere Instrumente ist auch dieses dem Wesen nach diskontinuierlich.

Die Quadranten haben mehrere Skalen. Die Skalen an der Nordseite und an der Südseite sind jeweils identisch. Auf der breiten Fläche der Quadranten sind Winkel aufgetragen, je nach Sternzeichen ist ein anderer Bereich von 180 Grad abgetragen. Auf der Schmalseite der Quadranten sind immer jeweils 15 Einheiten abgetragen pro Quadrant, das entspricht der alten indischen Einteilung des Kreises in 60 Ghatis bzw. des Tages in Abschnitte zu je 24 Minuten. Dabei ist die Null immer im Westen, die 15 immer im Osten aufgetragen. Oben auf der Schräge sind ebenfalls Skalen aufgetragen, auf beiden Seiten jeweils eine nach oben und eine nach unten laufende, die sich in der Mittelzone überlappen. Beim Cancer z. B. laufen diese 4 Skalen jeweils von Null bis 55.

Warum die verschiedenen Rampenneigungen?
Alle 12 Rampen und damit auch die zu den Rampen parallel geneigten Flächen der Quadranten haben eine unterschiedliche Steigung. Für die einzelnen Instrumente ergaben eigene behelfsmäßige Messungen folgende Werte:

Wichtig zum Verständnis des Systems ist:

• Die Steigung der Rampe ist maximal bei minimaler Sonnenhöhe.
• Und die Steigung der Rampe ist minimal bei maximaler Sonnenhöhe.
• Der Höchststand der Sonne im Sommer korreliert mit der ganz flachen Cancer-Rampe, die niedrige Sonnenstand im Winter korreliert mit dem steilen Capricorn-Instrument.
• Der in Jaipur zu beobachtende maximale Sonnenstand beträgt 90 + 23.5 (Ekliptik) - 27 (Breitengrad) = 86.5 Grad, die Neigung des Instrumentes wäre 27-23.5 = 3.5 Grad.
• Der in Jaipur zu beobachtende maximale Sonnenstand beträgt 90 - 23.5 (Ekliptik) - 27 (Breitengrad) = 39.5 Grad, die Neigung des Instrumentes wäre 27+23.5 = 50.5 Grad.

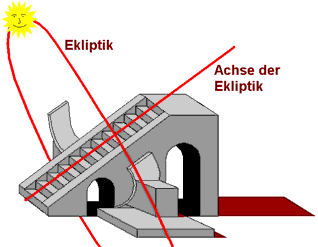
Nehmen wir noch einmal den oben beschiebenen Rotationskegel der Ekliptikachse um die Erdachse als Bezugspunkt, so, wie wir es auf der Erde wahrnehmen: Maximale Auslenkung nach hinten (von der Sonne weg) entspricht maximaler Ekliptik und minimaler Steigung für die Sommerinstrumente. Maximale Auslenkung nach vorne (zur Sonne hin) entspricht minimaler Ekliptik und maximaler Steigung für die Winterinstrumente. Wenn die Sonne genau über dem Äquator und damit im Himmelsäquator steht, ist die Steigung des Instrumentes gleich der geographischen Breite. Folgende Graphik illustriert die Geometrie von vier ausgewählten Instrumenten, die Sonne stehe in der Abbildung rechts:

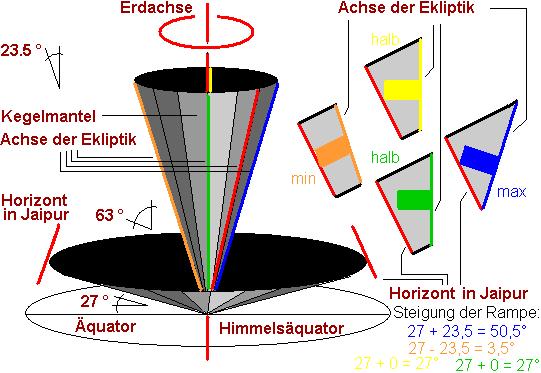
Warum stehen die Instrumente nicht alle parallel?
Betrachten wir noch einmal den seitlichen Versatz der Instrumente: Bei der scheinbaren Rotation der Achse der Ekliptik um die Erdachse gibt es nicht nur eine Höhenveränderung, sondern auch eine seitliche Veränderung. Denn sonst würde zwar die Rampe die Steigung richtig wiedergeben, aber die Ekliptikachse käme schräg auf der Rampe zu liegen. Die wird durch die versetzte Stellung der Instrumente in Relation zur Nord-Süd-Achse ausgeglichen.

• Genau in Nord-Südachse stehen die Instrumente für maximale und für minimale Sonnenhöhe, Cancer und Capricorn, jeweils in der mittleren Position auf dem Rotationskegel gelegen - von der Seite der Sonne (in der Abb. rechts) aus gesehen.
• Extremen seitlichen Versatz haben die Instrumente, die für die Bereiche der Tagundnachtgleichen gelten: Libra, Virgo, Pisces und Aries, wo die maximale seitliche Ausdehnung des Rotationskegels ausgereizt wird.

Folgende Graphik illustriert das für vier ausgewählte Instrumente:

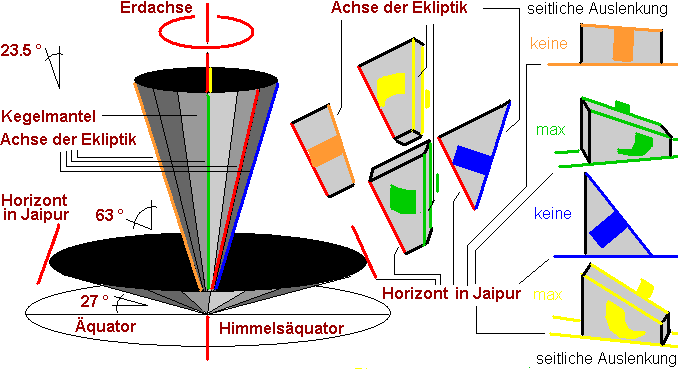
Photos, mehr Photos, noch mehr Photos, Nächstes Kapitel, Zurück zur Übersicht, Literatur zu indischer Astronomie
andere Essays über indische Kultur
Home

© Text, Graphik und Photos: Bernhard Peter 2005
Impressum