Bernhard
Peter
Jantar
Mantar - astronomische Geräte Indiens, Teil 16:
Das Laghu Samrat Yantra in Jaipur
Das Laghu Samrat Yantra ist die sogenannte "Kleine Sonnenuhr", klein in Bezug auf das riesige Samrat Yantra. Klein heißt aber nicht unbedingt schlechter, wie wir bei der Diskussion des Samrat Yantra gesehen haben. Es ist nur ein Viertel so groß wie das Samrat Yantra.
Konstruktion des Instrumentes:
Hauptbau ist ein Gnomon, ein
Sonnenzeiger in Form einer dreieckigen Rampe, mit einer Treppe
auf der Rampe. Ein wichtiger Unterschied zum Samrat Yantra ist,
daß auch auf der Nordseite eine Rampe mit einer Treppe ist. Die
Rampe endet oben in zwei Spitzen, die erst senkrecht abfallen und
dann in eine zweite, nördliche Rampe von ca. 39° Steigung
umknicken. Die Treppe ist auf ihrer ganzen Länge beiderseits von
einem Marmorband gesäumt. Das Gnomon ist genau entlang der
Nord-Süd-Achse ausgerichtet, mit dem hohen Ende nach Norden. Zu
beiden Seiten des Gnomons befinden sich zwei Quadranten wie
riesige marmorne Schwingen.

Was leistet das Laghu Samrat Yantra?
Der Hauptzweck war die
Bestimmung der Zeit nach dem Sonnenstand, also die Messung der
täglichen Sonnenbewegung (an den Quadrantenflügeln), und die
Messung der jährlichen Sonnenbewegung (entlang der Rampe). Mit
der aufsteigenden Sonne erscheint der Schatten zuerst auf der
linken äußeren Seite der Skala des westlichen Quadranten,
läuft dann mit steigender Sonne an der Marmorskala entlang
herab, taucht schließlich zur Mittagszeit unter dem Gnomon durch
(kein Schatten zu sehen) und läuft an der östlichen Skala
wieder hinauf, bis die Sonne am westlichen Horizont versinkt. Die
Quadrantenskalen erlauben das Ablesen der Uhrzeit und auch der
Länge des Tages. Die Skalen sind in Form eines weiten
Kreissegmentes gebogen und im Raum schräggestellt, damit sie
parallel zum Erdäquator sind, damit zu jeder Tageszeit ein
möglichst waagerechter Strich auf der Skala erreicht wird.
Deshalb ist die Skala für die späten Vormittags- und frühen
Nachmittagsstunden relativ flach, die für die frühen Morgen-
und späten Abendstunden (flache Sonne) aber relativ steil und
schräg. Aufgrund der Eigenbreite des Gnomons kommt eine weitere
Eigenart ins Spiel: Vormittags ist die westliche Außenkante des
Gnomons maßgeblich, nachmittags die östliche Außenkante. Die
Skala ist damit per se diskontinuierlich, was aber der
Genauigkeit keinen Abbruch tut. Auf der Westskala laufen die
Markierungen von 6 in 1-Stunden-Abständen bis 12, auf der
Ostskala von 12 bis 6. Ein Abschnitt einer Stunde ist erst in 4
Abschnitte zu je 1/4 h, dann weiter in je 3 Abschnitte zu je 5
Min, dann weiter in je 5 Abschnitte zu je 1 Minute und noch
einmal in je 3 Abschnitte zu 20 sec eingeteilt. Die Skalen sind
jeweils identisch am nördlichen und am südlichen Rand der
Marmorflächen aufgetragen.
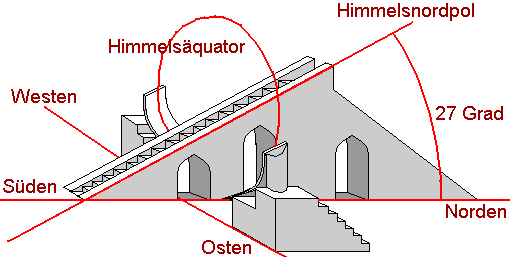
Die Rampe ist so gebaut, daß die Schräge genau parallel zur Erdachse steht. Jaipur liegt auf 27° geographischer Breite (genauer: Jaipur liegt auf 26°55'27'' Nord und 75°49'18.8'' Ost), folglich weicht der örtliche Horizont um ca. 27° von der Erdachse ab. Die Rampe (Hypotenuse des Dreiecks) korrigiert dieses wieder. Damit liegt die Rampe parallel zur Erdachse und deswegen weist der Blick entlang der Rampe direkt auf den Polarstern. Wenn dem nicht so wäre, würde der Schatten des Gnomons zu einer Vergleichsstunde zu verschiedenen Jahreszeiten in verschiedene Richtungen seinen Schatten werfen. Außerdem würde der Winkel, der in einer gegebenen Zeit durchschritten wird, ebenfalls von den Jahreszeiten abhängig sein. Die Parallelität von Gnomon und Erdachse ist damit eine fundamentale Voraussetzung für richtig gehende Sonnenuhren.
Über die Skala an der Rampe können wichtige Punkte im Jahr bestimmt werden. Denn die Sonnenbahn wird im Frühjahr immer steiler, erreicht ihren höchsten Punkt am Himmel zur Sommersonnenwende, und wird dann immer flacher, bis sie ihren tiefsten Punkt zur Wintersonnenwende erreicht. Die flügelartigen Skalen sind fest in Relation zur Rampe. Wenn die Sonnenbahn höher ist, wird ein anderer Abschnitt der Rampe auf die Skalen projiziert als im Winter, wo ein unterer Abschnitt projiziert wird. Durch Beobachtung der Projektionslinien und entsprechender Skalierung kann so an der Rampe ein Jahreskalender der Sonne abgelesen werden und können so die Sonnenwenden sowie die Tagundnachtgleichen bestimmt werden. Entsprechende Markierungen an der Rampe korrespondieren mit Linien auf den Quadrantenflügeln. Die Hypothenuse ist daher ebenfalls mit Skalen versehen, sowohl auf der rechten Kante als auch auf der linken Kante, einmal für die Vormittagsbebachtung, einmal für die Nachmittagsbeobachtung. Im Detail ist das noch ein bißchen komplexer: Auf jeder Seite sind genau zwei Skalen angebracht, eine beginnend bei Null oberhalb der Mitte und zum flachen Ende des Gnomons laufend bis 71, die andere unterhalb der Mitte mit Null beginnend und zum oberen (hohen) Ende des Gnomons laufend bis 63. In der Mitte sind die Skalenteile relativ klein, nach außen werden sie immer breiter. In der Mitte des Gnomons gibt es eine Zone, wo sich beide Skalen überlappen, in diesem Bereich springt die untere Skala nach innen und wird parallel in der Überlappungszone (0-20) weitergeführt. Jede Strecke von 10 Einheiten ist erst in zehn Abschnitte à 1 Grad, dann noch einmal in sechs Abschnitte und zuletzt noch einmal in 5 Abschnitte unterteilt.
Welchen Sinn macht das? Mit diesen Skalen kann man die Deklination der Sonne bestimmen. Der Schatten auf den Quadrantenskalen sieht immer gleich aus, unabhängig davon, welcher Teil der Kante ihn im Lauf eines Jahres wirft. Um festzustellen, welcher Teil der Kante den Schatten wirft, positioniert man an der Kante senkrecht zu dieser einen kurzen Schattenstab. Wenn er senkrecht zur Rampe steht, ist der Schatten genau parallel zur Kante des Quadranten. Man bewegt den Schattenstab nun an der Kante entlang, bis er genau an der Kante der Quadrantenfläche liegt- dann kann man an der Hypotenusen-Skala die Deklination der Sonne ablesen. Und in der einen Jahreshälfte nimmt man die eine Quadrantenskala und die nach oben laufende Hypotenusen-Skala, in der anderen Hälfte die andere Quadrantenskala und die nach unten laufende Hypotenusen-Skala. Soweit zur Sonne.
Mit Hilfe von Peilungen von der Quadrantenskala entlang der Rampenskala kann man auch beliebige andere Himmelskörper (Sterne, Planeten) anvisieren. An den Peilpunkten kann man jeweils die Positionsdaten ablesen. Die Größe des Gerätes ist geringer als die des Samrat Yantra, daher ist die Verwendung von Peilstäben und Peilschnüren denkbar. Das Anpeilen von Sternen geht nur folgendermaßen: Ein Beobachter steigt an der Quadrantenkante entlang, bis der Stern des Interesses genau über der Gnomonkante steht, er also die richtige Rektaszension gefunden hat, und fixiert dort mit der Hand den Stab oder die Schnur. Ein Helfer läuft mit mit dem anderen Ende die Treppe des Gnomons entlang und positioniert das jenseitige Ende der Peilhilfe solange neu, bis der Beobachter es in Linie mit dem Himmelsobjekt sieht. Nun kann der Helfer die Deklination ablesen. Hier ist wichtig, daß die Rampe genau parallel zur Erdachse verläuft und auf den Polarstern ausgerichtet ist, das System also auf Erdachse und Äquator basiert: Man erhält äquatoriale Koordinaten, nämlich Rektaszension (seitliche Abweichung) und Deklination (Höhenabweichung).
Interessant ist auch, daß das Laghu Samrat Yantra auf der Nordseite weitere Skalen entlang der Marmorbänder hat, die erst die senkrechte Fläche der beiden "Haken" herunterlaufen und dann der Schräge folgen. So etwas hat das goße Samrat Yantra nicht.
Ortszeit und indische Standardzeit
Die Sonnenuhr gibt Ortszeit
an, die für Jaipur gilt und der indischen Standardzeit
hinterherhinkt. Um auf indische Standardzeit zu kommen, muß man
bestimmte Korrekturwerte addieren:
| Monat/Tag | 5. | 10. | 15. | 20. | 25. | 30. |
| Januar | 32,10 | 34,18 | 36,13 | 37,50 | 39,09 | 40,08 |
| Februar | 40,52 | 41,06 | 41,06 | 40,38 | 39,58 | --- |
| März | 38,26 | 37,15 | 35,52 | 34,15 | 32,55 | 31,06 |
| April | 29,37 | 28,40 | 26,56 | 25,48 | 28,48 | 24,02 |
| Mai | 23,28 | 23,44 | 23,05 | 23,15 | 23,37 | 24,21 |
| Juni | 25,08 | 25,00 | 26,48 | 28,12 | 29,16 | 30,18 |
| Juli | 31,15 | 32,05 | 32,29 | 33,03 | 33,14 | 33,08 |
| August | 32,46 | 32,08 | 31,17 | 30,12 | 28,15 | 27,10 |
| September | 23,34 | 23,52 | 22,05 | 20,18 | 18,34 | 16,48 |
| Oktober | 15,18 | 13,54 | 12,39 | 11,38 | 10,56 | 10,28 |
| November | 10,25 | 10,43 | 11,22 | 12,24 | 13,44 | 15,24 |
| Dezember | 17,20 | 19,18 | 21,48 | 24,18 | 26,39 | 29,44 |
Photos, mehr Photos, Nächstes Kapitel, Zurück zur
Übersicht, Literatur
zu indischer Astronomie
andere Essays
über indische Kultur
![]() Home
Home
©
Text, Graphik und Photos: Bernhard Peter 2005
Impressum