Bernhard Peter
Jantar Mantar - astronomische Geräte Indiens, Teil 11:
Kleines Jai Prakash Yantra und Kapali Yantra in Jaipur

Das Gerät wird auch in das Kapali Yantra A im Westen und das Kapali Yantra B im Osten unterteilt. Das Kapali Yantra A entspricht einem kleinen Jai Prakash Yantra und dient dem Aufspüren der aktuellen Positionen vieler Himmelskörper, das Kapali Yantra B dient anderen Zwecken.

Konstruktion des Kapali Yantra A:
Das grundlegende Konzept des Jai Prakash Yantra ist die Abbildung der Himmelshalbkugel, wie wir sie wahrnehmen, auf einer inversen, d. h. hohlen Halbkugel, so als ob sämtliche Himmelskörper (Fixsterne, Planeten, Sonne) und ihre Bahnen wie durch Punktspiegelung auf einer hohlen Halbkugel projiziert werden. Das erspart langes Drehen und Peilen oder Warten auf die richtige Stellung, denn in die Halbkugel können die kompletten Bahnen eingezeichnet werden, samt diverser Koordinaten wie Azimut, Höhe (Horizontalkoordinaten) bzw. Deklination und Rektaszension (Äquatorialkoordinaten) und wichtiger Bezugspunkte wie Zenith und Himmelsnordpol – alles kann man in die Oberfläche gravieren. Genau das ist im kleinen Jai Prakash Yantra verwirklicht: In eine Plattform sind zwei halbe Hohlkugeln eingelassen, die jeden Skater zu wilden Phantasien anregen würde. Die marmornen Becken besitzen im Gegensatz zum großen Jai Prakash Yantra eine durchgehende Oberfläche und sind über und über mit Gravuren versehen, die die Bewegungen der Himmelskörper abbilden, natürlich invertiert, nach Punktspiegelung am Mittelpunkt der Kugel – also ist der Zenith am tiefsten Punkt der Halbkugel eingraviert und der Himmelsnordpol 27° vom Rand nach unten im Süden. Der Rand repräsentiert den Horizont. Mittels einer Drahtverspannung ist ein Ring genau im Inversionszentrum aufgehängt, dessen Schatten die Bahn der Sonne am Tage nachzeichnet.

Messung von Horizontalkoordinaten:
Die Plattform repräsentiert den Horizont; ein Drahtkreuz, das über die Halbkugel in Richtung der vier Himmelsrichtungen gespannt ist, gibt den Inversionspunkt für die Punktspiegelung in der Mitte vor. Konzentrische horizontale Linien im Becken geben die Höhe an, die Graduierung am Rand des Marmorbeckens gibt den Azimut-Winkel an. Nord und Süd ist mit 90 markiert, West und Ost mit 0°. Insgesamt ist es eine 360°-Einteilung, wobei jedes Grad noch einmal in 6 Abschnitte zu je 1 Pala unterteilt ist. Die Azimut-Linien tauchen senkrecht in das Becken hinab und treffen sich im eingravierten Zenith (illustriert im linken Teil der Zeichnungen).

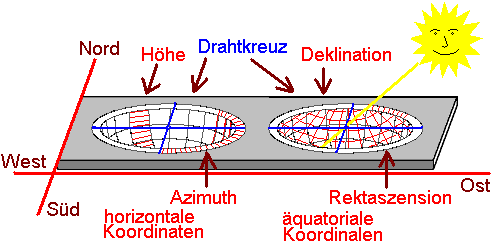
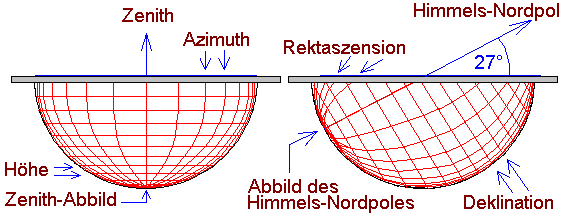
Messung von Äquatorialkoordinaten:
Der Bezugspunkt ist jetzt nicht mehr der Zenith, sondern der Himmelsnordpol, nicht mehr der Horizont, sondern der Himmelsäquator. Hier kommt Jaipurs geographische Breite ins Spiel, 27°. Um genau diesen Winkel liegt der Himmelsnordpol auf dem Nord-Süd-Meridian nach Süden verschoben im Marmor-Abbild. Die nun relevanten Linien sind konzentrische Kreise um das Abbild des Himmelsnordpoles, die die Deklination angeben, senkrecht dazu die Linien für die Rektaszension (illustriert im rechten Teil der Zeichnungen). Im Original umfaßt das Liniennetz beide Arten von Koordinaten in Überlagerung.

Funktion und Grenzen:
Der Ring, der im Mittelpunkt der Halbkugel von den in Nord-Süd- und West-Ost-Richtung gespannten Drähten gehalten wird, dient als Fixpunkt der Beobachtung. Einfach ist die Beobachtung der Sonne: Der Schatten des Ringes zeichnet seine Bahn durch die Halbkugel und erlaubt direkt das Ablesen der Koordinaten in beiden Systemen. Die Informationen, die man erhält, sind neben den Sonnenkoordinaten die lokale solare Zeit, Sommer- und Winter-Sonnenwende, Tagundnachtgleichen und Tierkreiszeichen. Bei Sternen gestaltet sich das schon erheblich schwieriger, da die damalige Technologie keine Projektion der Sterne auf die Schalenwand erlaubte. Für die Sternbeobachtung hätte die Schale aus transparentem Material sein müssen.

Kapali Yantra B:
Das Kapali Yantra B ist die baugleiche zweite Hemisphäre im Osten. Sie wurde nicht zum Beobachten der Sonne verwendet, sondern sie war ein Abbild der Planetenbewegungen und diente der graphischen Lösung astronomischer Probleme. Die Schale hat verschiedene Punkte am Rand markiert, von denen jeweils Meridianlinien zum gegenüberliegenden Rand verlaufen. Insgesamt ist es eine 360°-Einteilung, wobei jedes Grad noch einmal in 6 Abschnitte zu je 1 Pala unterteilt ist. Von 6 Punkten ausgehend wird je ein vollständiges Liniennetz aufgespannt, dies sind die vier Himmelsrichtungen (Süden und Norden = 0, Osten und Westen = 90) sowie 26.9° in SW bzw. NO-Richtung, also insgesamt 3 Meridiansysteme. 5 weitere Systeme mit jeweils nur drei Linien verbinden die Punkte bei 42.9°, 51.6°, 63.1°, 74.6° und 83.3° von SO nach NW. Alle diese Netze überlagern sich und formen ein hochkomplexes Liniennetz.

Photos, Nächstes Kapitel, Zurück zur Übersicht, Literatur zu indischer Astronomie
andere Essays über indische Kultur
Home