Bernhard Peter
Jantar Mantar - astronomische Geräte Indiens, Teil 8:
Das Digamsa Yantra in Jaipur

Konstruktion des Instrumentes:
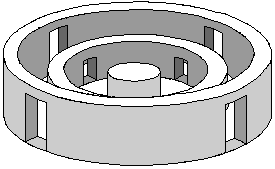
Auf einer ebenen Fläche befindet sich eine zylindrische zentrale Säule, die von zwei konzentrischen kreisförmigen Wänden umgeben ist, wovon die innere etwa gleich hoch ist wie die Säule (1 m), die äußere Wand jedoch fast doppelt so hoch ist wie die beiden anderen Strukturelemente (ca. 2 m). Die Oberkante von Säule und Wänden ist mit Marmor belegt, in den Skalen eingraviert sind, an denen man den Azimut-Winkel ablesen kann. Diese Skalen repräsentieren den Horizont wie um einen gigantischen Kompaß herum. Der Durchmesser des gesamten Systems beträgt ca. 8 m. Beide Ringe haben jeweils 4 Öffnungen, wovon nur die im äußeren Ring wirklich begehbar sind. Die Mittelsäule hat eine umlaufende Skala, der innere Ring hat insgesamt 4 Skalierungen, innen und außen, sowohl auf der Fläche als auch auf der Senkrechten, und schließlich der äußere Ring hat zwei Skalen, innen und außen auf der Senkrechten, aber keine auf der horizontalen Fläche. Die Skala des inneren Ringes läuft jeweils von Null in Süd und Nord bis 90 Grad in Ost und in West, die Ziffern sind in Zehnerschritten eingraviert. Zwei dezimale Unterteilungen der Gradstriche ergeben eine Ablesegenauigkeit von 0.01 Grad. 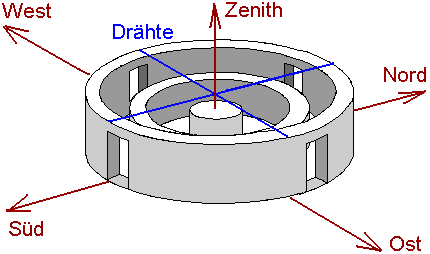Über das ganze System wurden zwei sich rechtwinklig schneidende Drähte gespannt, einer in Nord-Süd-Richtung, einer in West-Ost-Richtung. Der Schnittpunkt beider Drähte (Ringöffnung) kam exakt über der zentralen Säule zu liegen, die senkrechte Verbindungslinie ist in einer Linie mit dem Zenith. Eine andere Möglichkeit wäre die Errichtung eines senkrechten Stabes in der Mitte der Zentralsäule.

Was leistet das Digamsa Yantra?
Der Schwerpunkt dieses Gerätes ist die Winkelbestimmung. Das System basiert auf Horizont und Zenith. Man erhält in erster Linie den Azimut-Winkel, und zur Azimut-Bestimmung ist dieses Instrument das Genaueste. Die Winkelbestimmung ist im Gegensatz zum Rama Yantra lückenlos möglich, dafür sieht dieses Gerät keine Höhenmessung vor. Die praktische Nutzung ist auf vielerlei Weise möglich.

Z.B., zur Bestimmung des Azimutwinkels der Sonne, kann man von der Mitte der Säule zur Skala einen Faden spannen oder einen Peilstab legen und diesen so lange verschieben, bis er sich mit dem Schatten des Kreuzungspunktes deckt. Dann kann man an der Skala den Winkel ablesen.

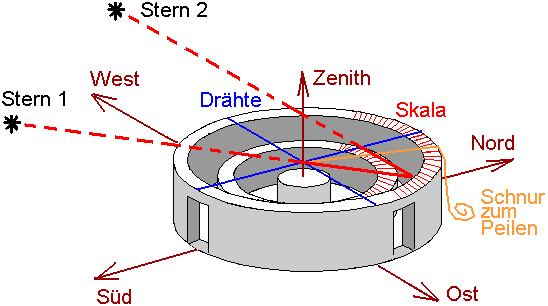
Eine Möglichkeit des praktisches Vorgehens zur Winkelmessung von Sternen ist die folgende: Der Beobachter steht zwischen den beiden konzentrischen Mauern, ein Helfer außerhalb der äußeren Mauer. Die Person außerhalb hält einen Hilfsfaden, der an dem Kreuzungspunkt der beiden Drähte als Peilhilfe befestigt wurde. Beide Personen stellen sich ungefähr gegenüber dem zu bestimmenden Stern auf. Über den Rand der inneren Mauer und den Kreuzungspunkt der Drähte kann ein Stern nur genau angepeilt werden, wenn er sich in einer bestimmten Höhe befindet (Stern 1). Hat der Stern eine andere Höhe (Stern 2), wird der Hilfsfaden gebraucht: Der äußere Helfer verschiebt den Faden so lange, bis Stern, Kreuzungspunkt der Drähte und Faden in einer Linie stehen. Dann kann der Winkel an der Skala abgelesen werden, sowohl dort, wo der Faden auf der äußeren Mauer aufliegt, als auch an der Kante der inneren Mauer, von wo der Beobachter Stern, Kreuzungspunkt und Faden anpeilt. Noch komplizierter wäre es, an dem horizontalen Hilfsfaden einen zweiten Hilfsfaden zu befestigen, dessen Knoten man entlang des ersten Hilfsfadens verschiebt, bis die Höhe stimmt, und den man dann an der inneren Skala anlegt. Durch synchrones Verschieben beider Auflagepunkte (müssen an der selben Winkelmarke liegen) läßt sich die zutreffende Winkelmarke finden. Oder ganz einfach: Man spannt den Visierfaden von der Mitte der Zentralsäule und zieht ihn über die äußere Mauer. Der Beobachter peilt von der Kante der Skala aus nach oben und läßt seinen Helfer so lange den Faden verschieben, bis der Faden genau den Stern des Interesses überdeckt. Es gibt viele Möglichkeiten!

Photos, Nächstes Kapitel, Zurück zur Übersicht, Literatur zu indischer Astronomie
andere Essays über indische Kultur
Home