Japanische Kunst und Kultur

Bernhard Peter
Typisch japanische Dinge (30): Igo - Go-Spiel

Ein Go-Brett (Goban) besitzt 19 x 19 Linien. Zur Illustration wird hier in den Abbildungen nur ein Ausschnitt verwendet. Es ist aber auch möglich, ein kleineres Feld von nur 13 x 13 Linien zu verwenden. Die Steine werden von den Spielern abwechselnd auf die Kreuzungspunkte gesetzt. Schwarz beginnt. Auch die Ecken und die Randkreuzungspunkte sind mögliche Steinpositionen und können benutzt werden. Einige wenige Kreuzungspunkte sind auf dem Brett besonders hervorgehoben - das hat mit einem gewährten Spielvorteil zu tun, bei dem die Vorgabesteine dort plaziert werden. Im Spielverlauf sind diese hervorgehobenen Kreuzungspunkte den normalen Kreuzungen gleich. Die Linien werden 1-19 bzw. a-t bezeichnet. Der Mittelpunkt des Brettes ist also k10, die linke untere Ecke a1. Gespielt wird mit hellen, typischerweise weißen, und dunklen, typischerweise schwarzen, Steinen. Da das Brett insgesamt 361 Schnittpunkte besitzt, benötigt man maximal 360 Steine, also besitzt jeder Topf 180 Steine einer Farbe. Die Steine sind in der Aufsicht rund und im Querschnitt ellipsenförmig.

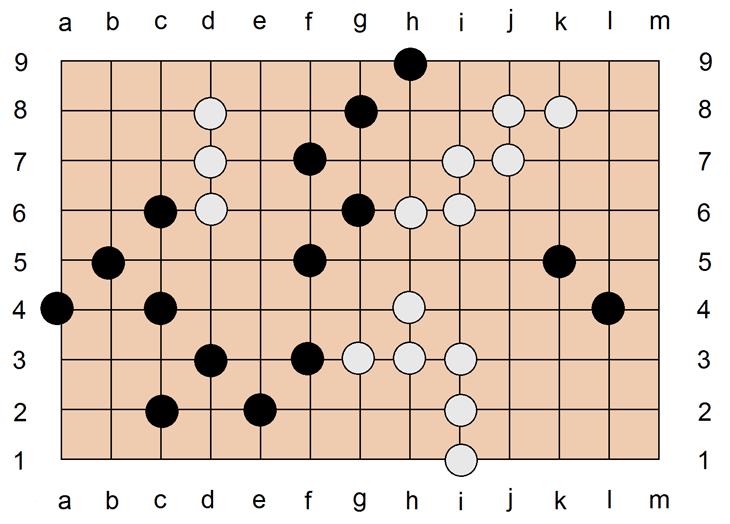
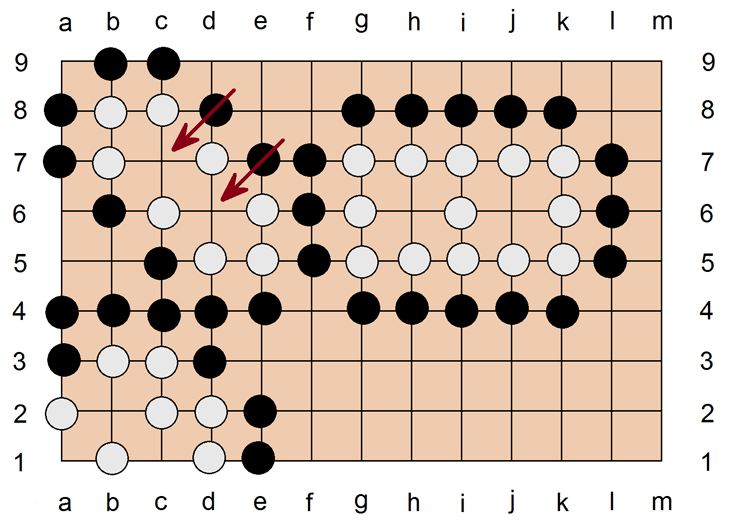
Steine, die unmittelbar nebeneinander liegen, also auf horizontal oder vertikal benachbarten Plätzen positioniert sind, sind verbundene Steine. Im obigen Beispiel bilden alle weißen Steine verbundene Steingruppen. Es ist nicht möglich, eine solche Kette mit einer gegnerischen Kette zu durchbrechen oder zu kreuzen. Es ist nicht möglich, einzelne Steine durch Umzingeln (s. u.) aus einer solchen engen Kette herauszuschneiden. Steine, die diagonal benachbart sind, sind unverbundene Steine. Im obigen Bildbeispiel sind alle schwarzen Steine unverbundene Steine. Schräge Aneinanderreihung schafft keine Verbindung. Es ist möglich, eine solche Kette mit einer gegnerischen Kette zu kreuzen, und es ist auch möglich, einzelne Steine durch Umzingeln (s. u.) aus einer solchen lockeren Kette herauszuschneiden.

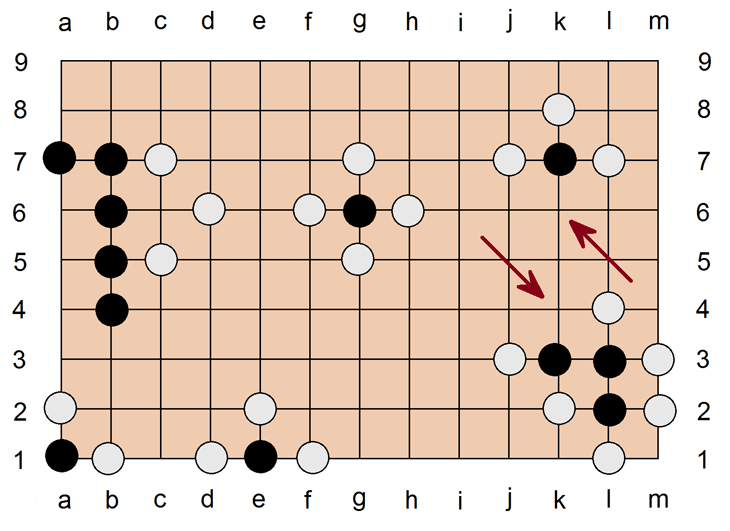
Ein wichtiges Prinzip, um die Dominanz über die Spielfläche zu erhalten, ist das Umzingeln fremder Steine. Ein Stein gilt als umzingelt, wenn er ringsum von Steinen der anderen Farbe umgeben ist. Dabei zählen gerade und diagonale Verbindungen, aber nur direkte. D. h. die Umzingelung muß lückenlos sein: In der umzingelten Fläche darf kein freier Platz übrig bleiben, sonst ist die Einschließung nicht komplett. Ein Stein oder eine zusammenhängende Gruppe von Steinen gelten als umzingelt, wenn alle benachbarten Kreuzungspunkte lückenlos von Fremdsteinen besetzt sind. Im obigen Bild sind die schwarzen Steine a1, e1 und g6 vollständig umzingelt. Zum vollständigen Einschluß sind also im Feld 4, am Rand 3 und in der Ecke 2 Steine notwendig. Umzingelte Steine werden umgehend vom Spielbrett genommen und als "Gefangene" zur Seite gelegt. Der Zustand wie oben kann nicht über den Zug hinaus existieren, denn Setzen und Herausnehmen sind ein einziger Zug. Beide Aktionen gehören zusammen. A1, e1 und g6 hätten sofort nach Setzen des letzten einschließenden weißen Steines herausgenommen werden müssen. Steine ohne "Freiheiten", also ohne angrenzende freie Punkte, können auf dem Spielbrett nicht existieren. Deshalb darf man auch keinen Zug machen, der dazu führen würde, daß die eigenen Steine keine Freiheiten mehr besitzen (Selbstmord). Um k7 herausnehmen zu können, muß Weiß am Zug k6 setzen. Um k3, l3 und l2 herausnehmen zu können, muß Weiß am Zug k4 setzen. Weiß wird sich immer für den Zug entscheiden, der den größten Gebietsgewinn bringt, der also die meisten freien oder freiwerdenden Plätze unter die eigene Dominanz bringt.

Es kann manchmal sinnvoller sein, große Flächen zu sichern, als einzelnen Steinen des Gegners hinterherzujagen. Wenn Weiß k4 setzt und die drei schwarzen Steine herausnimmt, bleiben die Lücken in der Regel offen, denn es wäre für Schwarz Verschwendung, hier noch mal etwas zu versuchen, wenn die Fläche so klein ist wie hier. Bei teilumzingelten Steinen kann der teilumzingelte Spieler versuchen, durch Anlegen Verbindung zu anderen Steingruppen zu schaffen oder durch Erzeugung von "fliehenden Diagonalen" zur Mitte hin komplexe Strukturen vorzubereiten. Sollte das insbesondere bei randnahen Situationen oder in Situationen mit vielen gegnerischen Blockaden nicht möglich sein, ist es selten sinnvoll, anzulegen, weil man de facto seinen Verlust noch vergrößert. Beispiel: In der obigen Situation könnte Schwarz am Zug also eine Verbindung von k3 zu k7 aufbauen und dann nach links ausbrechen. Da Schwarz für die Verbindung 3 Steine braucht, Weiß aber für die Umzingelung 5 Steine, wäre das theoretisch möglich. Andererseits wird Weiß klugerweise erst nur auf der j-Linie den schwarzen Steinen auf der k-Linie folgen, und Schwarz am Zug muß sofort entweder k4 oder k6 setzen. Weiß wird dann den jeweils anderen Punkt nehmen und 1 oder 3 Steine Beute machen. Deshalb könnte Schwarz k4 setzen. Weiß folgte dann mit k6. Schwarz kontert mit j4 und hätte die Möglichkeit zum Ausbruch. Deshalb wird Weiß nach k4 statt dessen j4 setzen, nach zwingend folgendem k5 nun j5, nach erneutem k6 schließlich j6. Schwarz kann nun nur noch nach rechts anlegen, wo man wegen der bereits vorhandenen weißen Steine l4 und l7 nur zwei Züge braucht, um den "Sack zu verschnüren". Auf Schwarz l5 folgt Weiß l6, auf Schwarz m5 folgt Weiß m6 etc. Aufgrund er vielen vorhandenen weißen Steine kann Schwarz nicht wirklich ausbrechen und verliert irgendwann alles, wodurch das gesamte Territorium an Schwarz fällt. Es wäre also von Anfang an klüger gewesen, die schwarzen Steine aufzugeben und woanders Vorsprung aufzubauen, während Weiß die Umzingelung vollendet.

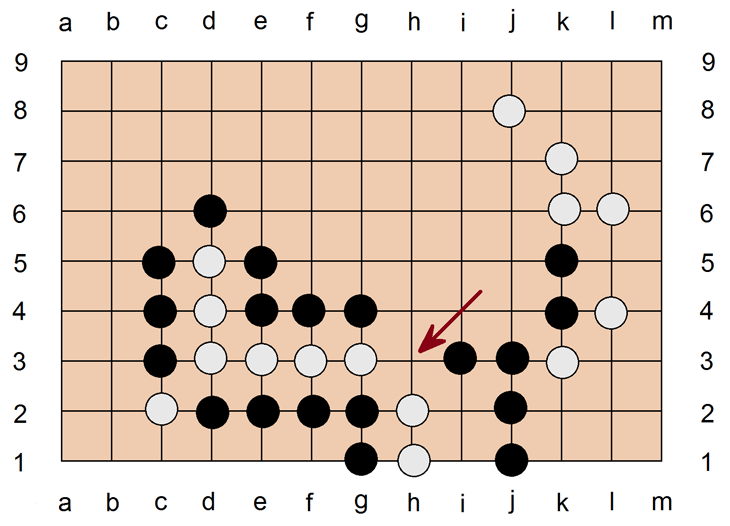
Da Go-Spiel besteht also im wesentlichen aus dem Ausbau des dominierten Territoriums einerseits und einem Umzingelungskampf an den Territorialgrenzen andererseits. Es ist wichtig, daß eine Umzingelung nur dann gilt, wenn sie lückenlos ist. Wenn Schwarz am Zug h3 setzt, sind d3, d4, d5, e3, f3 und g3 vollständig umschlossen. Nicht aber h1 und h2 - diese beiden Steine sind zwar reihum von schwarzen Steinen umgeben und im Grunde chancenlos, weil sie nie mehr eine Anbindung an andere weiße Strukturen bekommen werden, aber sie sind nicht umzingelt und dürfen nicht herausgenommen werden.

Solange in einer Stellung ein freier Platz (Auge) besteht, kann dieser besetzt werden. Das kann man benutzen zum Sprengen fremder Stellungen. Schwarz am Zug kann a1 besetzen. Das ist eigentlich ein unmöglicher Zug, weil der Platz völlig von Weiß umzingelt ist. Wenn man aber damit seinerseits den Gegner völlig umzingelt, ist das möglich: Weiß setzt in a1 und nimmt a2, b1 und b2 heraus. Ebenso kann Schwarz alternativ g1 besetzen und d1, e1 und f1 herausnehmen. Sprengen bedeutet, daß man einen inneren Punkt besetzt, nachdem die äußere Umzingelung vollendet ist. Bei mehreren Plätzen ist das erheblich schwieriger - Bsp. Schwarz auf a6. Nur wenn Weiß mit a5 oder a7 kontert, kann die Sprengung durch Schwarz dann mit a7 oder a5 gelingen. Reagiert Weiß nicht und setzt statt dessen d5 o.ä., kann Schwarz nicht weiter arbeiten, denn mit Schwarz auf a5 oder a7 würde es sofortigen Verlust zweier Steine im nächsten Zug von Weiß auf a7 oder a5 riskieren. Schwarz auf a6 ist also keine sinnvolle Option bei dieser Stellung.

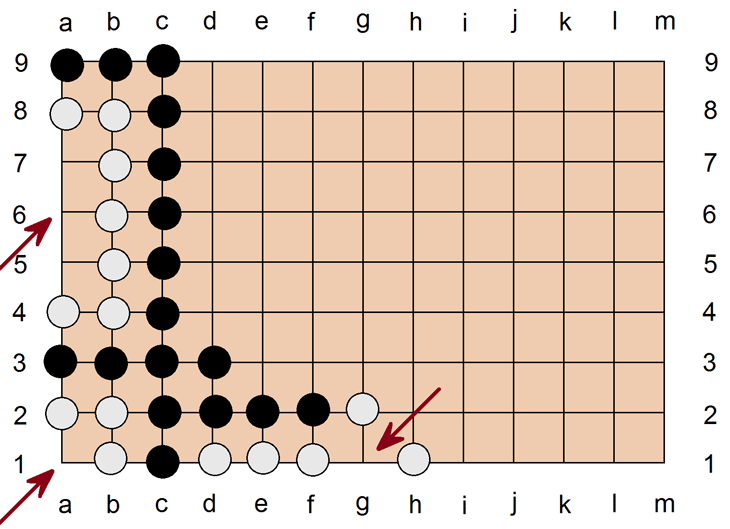
Wie wir gesehen haben, lassen sich Stellungen mit EINEM Auge sprengen, wenn sie außenherum komplett eingeschlossen sind und der finale Stein in das Auge gesetzt wird. Es ist aber unmöglich, Stellungen mit ZWEI oder mehr Augen zu sprengen, wenn sie eine geschlossene Außenbegrenzung haben. Die weißen Stellungen links unten und rechts oben sind absolut uneinnehmbar für Schwarz. Es gibt keine Möglichkeit des Sprengens, und es gibt auch keine Möglichkeit, so eine Stellung von außen anzunagen, weil alle Steine verbunden sind. Anders sieht es in der Stellung links oben aus. Auch hier gibt es zwei Augen, doch diese Stellung ist nicht uneinnehmbar, weil die äußeren Begrenzungen nicht verbundene Steine sind. Schwarz kann mit d6 oder c7 jeweils drei Steine erbeuten und im nächsten Zug noch einmal 5 Steine. Es gibt für Weiß keine Chance, das zu verhindern.

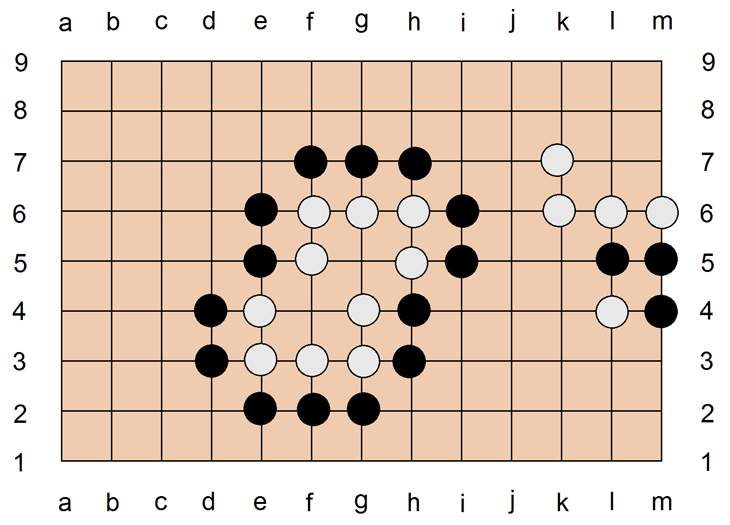
Die oben abgebildete Stellung hat nur zwei weiße Steine mehr als die vorherige, ansonsten aber die selbe Situation mit zwei Augen und nicht überall verbundenen Steinen. Dennoch kann diese Stellung nicht gesprengt werden, weil Schwarz keine beidseitige diagonale Anbindung des sprengenden Steines schafft. Diese Stellung ist für Weiß absolut sicher.

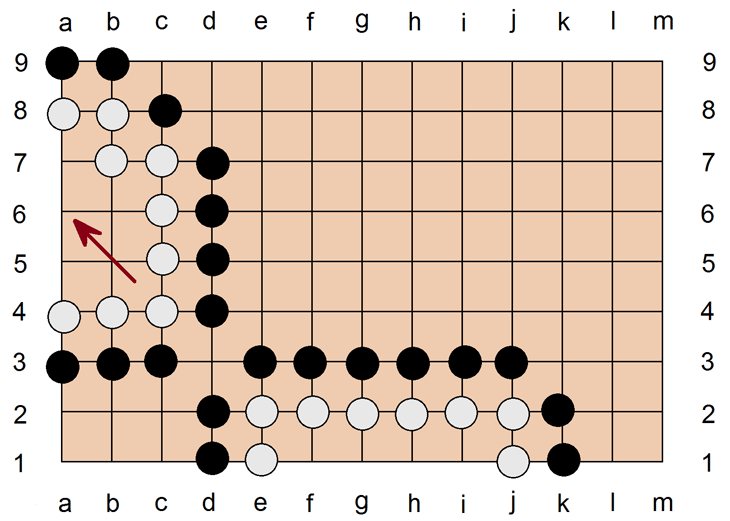
So wie man selbst versucht, doppelte Augen zu erzeugen, um seine Stellungen abzusichern, so versucht man andererseits, doppelte Augen beim Gegner zu verhindern. Im obigen Beispiel kann Schwarz in der unteren Stellung das Entstehen doppelter Augen für Weiß jedoch nicht mehr stoppen: Weiß auf f1 und i1 geht nicht, das wäre Selbstmord im nächsten Zug von Weiß. Also Versuch auf g1 oder h1, mit der Folge Weiß auf h1 oder g1, und im nächsten Zug auf Weiß auf f1 und i1, Stellung hat zwei Augen und ist uneinnehmbar. Anders ist das bei der Stellung links oben: Hier könnte Schwarz auf a6 gehen, und langfristig geht möglicherweise die Stellung für Weiß verloren, weil sich keine zwei Augen mehr für Weiß bilden lassen. Wichtig ist lediglich, daß irgendwann nur ein freier Platz übrig bleibt, wenn Schwarz danach am Zug ist. Wenn Weiß aber bei zwei freien Plätzen abwartet, kann Schwarz die Stellung nicht lösen, und der Versuch wird als verlorene Steine enden. Steine oder Ketten werden als lebendig bezeichnet, wenn sie vom Gegner nicht weggenommen werden können, oder wenn ihre Umzingelung und Wegnahme einen neuen gegnerischen Zug ermöglichen würde, der nicht zu einem wegnehmbaren Stein führt. Steine oder Ketten, die nicht lebendig sind, werden als tote Steine oder Ketten bezeichnet (spielt bei der Auswertung eine Rolle).

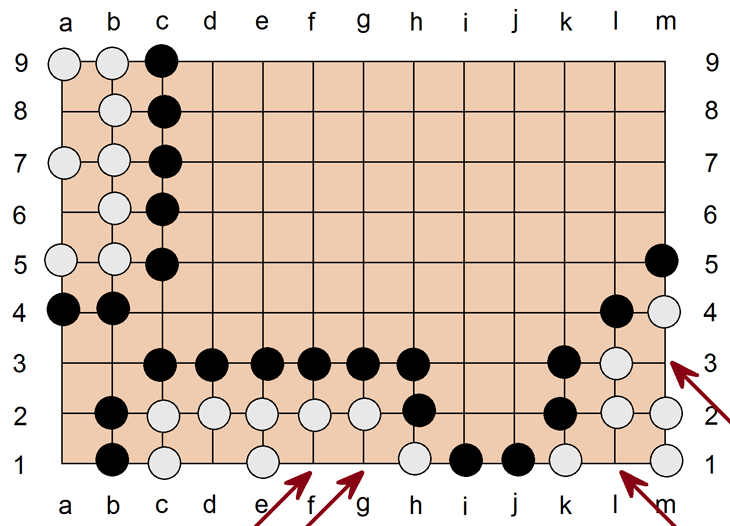
Es gibt echte und unechte Augen: Echte Augen haben genau einen freien Platz, der vollständig von einer verbundenen Kette einer Farbe umschlossen ist. In der obigen Abb. sind echte Augen bei a8, a6, d1. Das Auge f1 und g1 hingegen ist ein unechtes Auge. Deshalb ist die Stellung links oben sicher und geschützt, die Stellung unten nicht. Schwarz am Zug könnte g1 setzen und h1 nehmen. Weiß dürfte nicht direkt danach h1 setzen, sondern würde woanders setzen müssen, Schwarz würde erst h1, dann f1 und schließlich d1 setzen und die ganze weiße Stellung räumen. Auch die weiße Stellung rechts im Bild ist trotz zweier Augen nicht sicher, weil Schwarz durch l1 oder m3 jeweils ein Auge vernichten könnte.

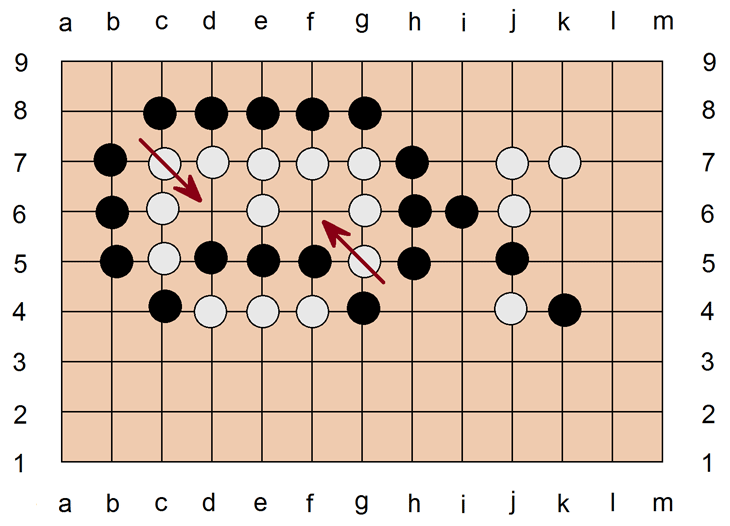
"Seki" bezeichnet eine Stellung, in der es keine Partei wagen kann , einen Punkt an der Grenze zweier Territorien zu besetzen. Weder Schwarz noch Weiß kann hier auf d6 oder f6 gehen, ohne den Verlust von c5, c6, c7, d7, e6, e7, f7, g5, g6, g7 für Weiß bzw. d5, e5, f5 für Schwarz und dem zuletzt gesetzten Stein zu riskieren. Wir haben also hier den Sonderfall, daß eine Kette keine zwei Augen bildet, aber dennoch nicht gesprengt werden kann. Weil diese Punkte bis zum Schluß des Spieles nicht besetzt werden können, bleiben sie frei und zählen bei der Endabrechnung für keine der beiden Parteien.

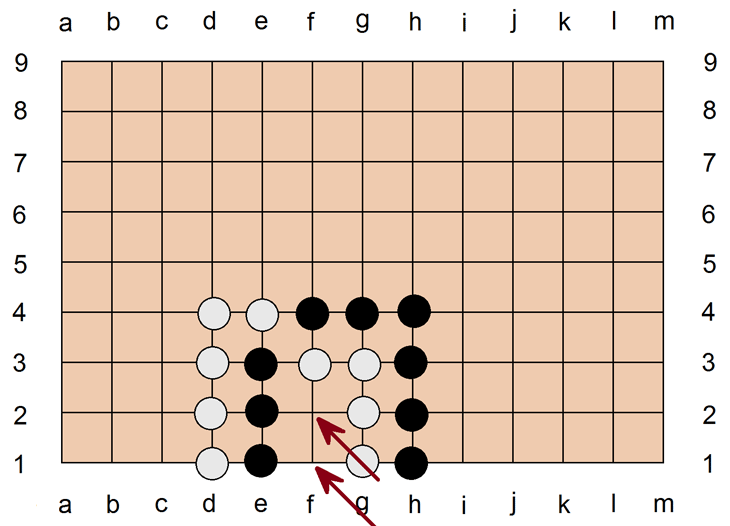
Auch diese Konstellation ist "Seki": Weder Weiß noch Schwarz kann riskieren, f1 oder f2 zu besetzen, ohne im nächsten Zug Steine zu verlieren, im Falle von Weiß 4+1 Steine, im Falle von Schwarz 3+1 Steine. Deshalb werden die Spieler eine solche Situation bis zum Spielende unverändert so lassen.

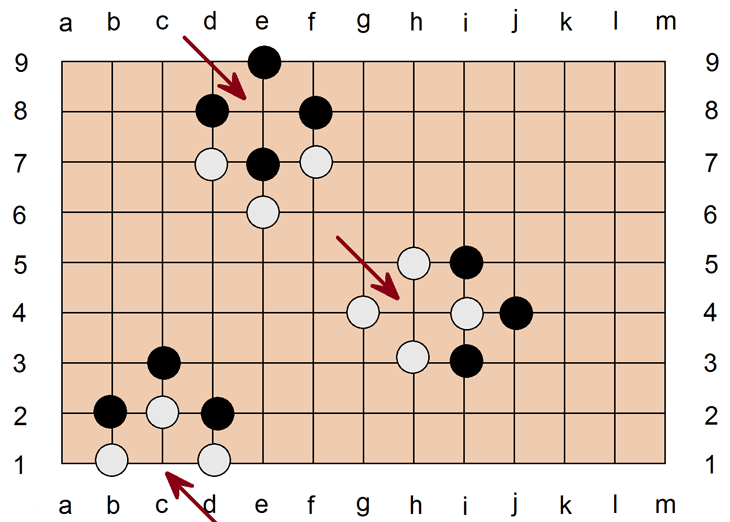
"Ko" ist eine Stellung, die zur Endlosschleife werden könnte. Im obigen Bsp. sind drei verschiedene Ko-Stellungen zu sehen. Schwarz auf c1 oder h4 würde c2 oder i4 erbeuten. Daraufhin könnte anschließend Weiß auf c2 oder i4 gehen und jeweils einen schwarzen Stein erbeuten. Usw. Sonne geht unter, Sonne geht auf.... Im Falle e8 und e7 könnte man mit Weiß am Zug das Gleiche machen. Dieser Endlosabtausch ist phantasielos und bringt keiner Partei etwas. Deshalb gibt es da eine Regel: Wenn mit einem Stein ein anderer feindlicher Stein genommen wird, darf dieser nehmende Stein im anschließenden Zug nicht wieder selbst genommen werden. Das heißt, daß eine solche zyklische Endlosschleife verboten ist. Es darf keinen Zug geben, der zur Wiederholung der gesamten Brettsituation mit dem selben Spieler am Zug führt. Wenn Schwarz auf h4 geht und i4 nimmt, darf Weiß erst im übernächsten Zug wieder auf i4 gehen, wenn Schwarz nicht selbst i4 zwischenzeitlich mit einem eigenen, also schwarzen Stein blockiert hat.

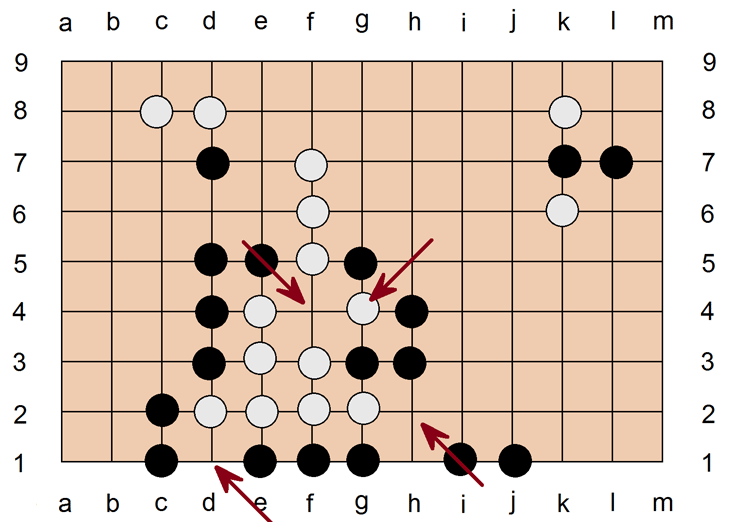
Selten tritt eine Ko-Situation so isoliert auf wie in den Stellungen der vorletzten Abbildung. Die obige Abbildung zeigt eine realistischere Ko-Stellung, wo das Ko Teil einer größeren Stellung ist. Wenn Schwarz den Ko-Kampf um f4/g4 gewinnt, kann Schwarz langfristig d2, e2, f2, g2, e3, f3 auch noch abräumen. Deshalb muß Weiß zuerst f4 besetzen und sein Auge vernichten, um den rettenden Anschluß an f5, f6, f7 zu bekommen; von da geht es gegen den Uhrzeigersinn um die schwarze links Stellung herum. Wenn es Schwarz gelingt, f4 zu bekommen, ist für Weiß die Stellung verloren, es sei denn, Weiß kann im nächsten Zug woanders eine so große Drohung aufbauen, daß Schwarz lieber dort reagiert und diese sieben weißen Steine sausen läßt. Es bleibt für die Parteien eine Abwägung, ob es vorteilhafter ist, auf eine Drohung zu reagieren oder das Ko zu schließen. Die Kunst besteht darin, vorteilhafte Ko-Stellungen anzulegen, denn das bedeutet de facto, daß man an einer interessanten Stellung zwei Züge hintereinander machen darf.

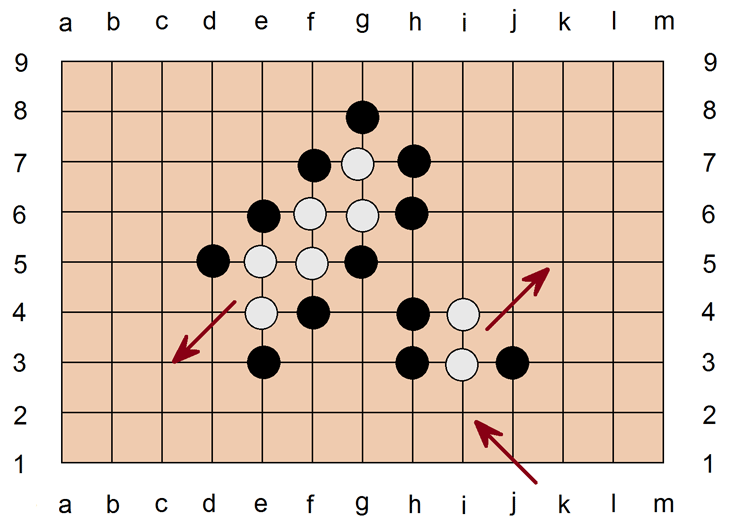
Wenn man umzingelt wird, kann man durch Anlegen von Steinen seine Stellung verlängern. Man bildet einen sog. schrägen Balken, in der obigen Abb. ist das Weiß. Wegen der drohenden Gefahr von Diagonalen müssen alle Steine verbunden sein. Das heißt, Verteidiger (Weiß) und Angreifer (Schwarz) brauchen für jede Extension des schrägen Balkens zwei Steine. Es kann also endlos so weiter gehen - außer bis zum Rand: Denn Sobald Weiß an den Rand kommt, macht Schwarz den "Sack zu", denn Weiß konnte keine Augen aufbauen. Daher ergibt es nur einen Sinn, einen schrägen Balken zur Mitte hin zu entwickeln oder in Richtung auf eine andere eigene Stellung. Im rechten Beispiel kann Schwarz durch i2 Weiß dazu bewegen einen schrägen Balken nach rechts oben aufzubauen. In dieser Lage täte Weiß gut daran, durch einen Fernzug in diese Richtung, z. B. l7, vorzubeugen - denn dann hätte der schräge Balken eine Chance, wenn er auf einen weißen Außenposten hin ausgebaut werden könnte.

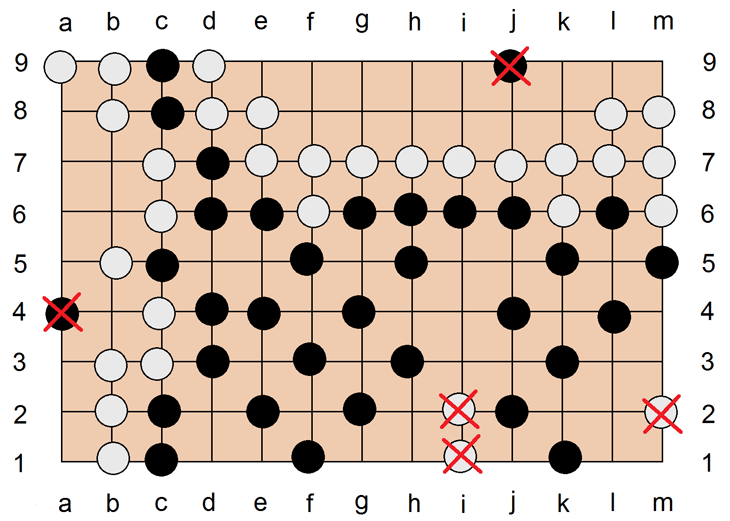
Wann ist das Spiel beendet? Wenn beide Spieler nacheinander passen. Wenn also kein Spieler eine sinnvolle Stelle für seinen nächsten Zug findet. Das Spiel endet, wenn die weißen und schwarzen Territorien durch eine beidseitig lückenlos geschlossene Grenze eingerahmt werden, also an der Grenze kein besetzbarer Platz frei ist (Ausnahme: Seki, s. o.). In der obigen Abb., Ausschnitt eines kompletten Spielbrettes, lassen sich deutlich drei Territorien erkennen, zwei kleine weiße und ein großes schwarzes (weil es ein Ausschnitt ist, ist c8/c9 möglich). Ein paar wilde Steine und tote Ketten sind zu erkennen, allein gelassene Steine ohne Anbindung an eigenes Territorium, mitten in Feindesland.

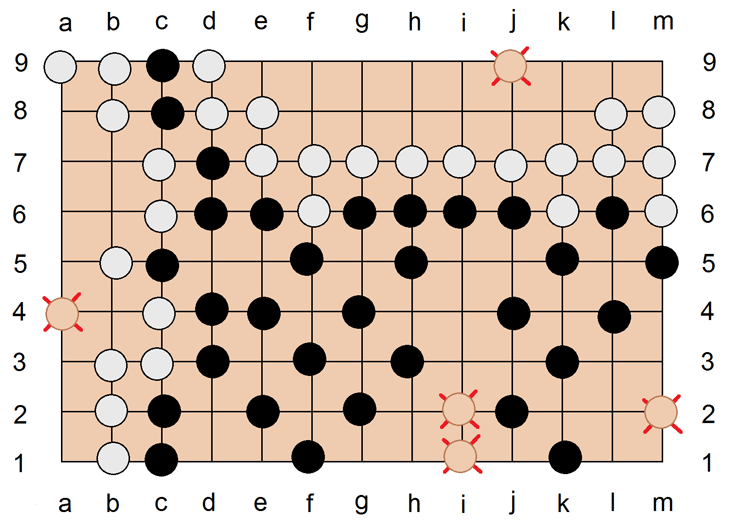
Es würde rechnerisch nichts bringen, um diese Positionen zu kämpfen. Deshalb werden die wilden Steine einfach herausgenommen. Danach nimmt man die herausgenommenen wilden Steine und die vorher im Spielverlauf gefangenen Steine und legt sie dem Gegner irgendwo in seinem Territorium auf freie Plätze. Man kann auch noch innerhalb eines Territoriums die Positionen zu Zehnerketten umordnen, das macht das Zählen leichter.

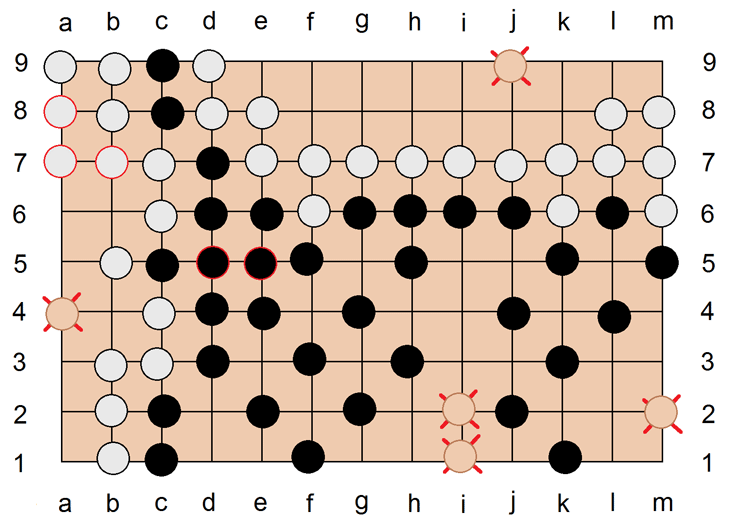
Es ist leicht nachzuvollziehen, daß sich dadurch nichts am Ergebnis ändert, daß aber die Auszählung einfacher wird. Für jeden Spieler werden nun die freien Augen in seinem Territorium gezählt, also die leeren Punkte, die nur von eigenen Steinen umrandet sind. Seki-Positionen werden nicht gezählt. Es gibt noch Komi: Der Spieler Weiß bekommt 6,5 Steine als Ausgleich dafür, daß Schwarz beginnt. Die Differenz zwischen beiden Zahlen gibt das Ausmaß des Sieges an (japanische Wertung). Manchmal gibt es umstrittene Gebiete, dann ist eine Schlichtung nötig, ggf. unter Wiederaufnahme des Spiels im strittigen Gebiet. Bei Wiederaufnahme beginnt der andere Spieler als der, welcher die Wiederaufnahme gefordert hat.

Daneben gibt es noch etliche andere Regelsysteme, chinesische, koreanische etc. In Deutschland orientiert man sich an den japanischen Regeln in leicht modifizierter Form. Die unten angegebenen Links führen zu vertiefenden Darstellungen mit vielen weiteren Spielsituationen in den Kommentaren.

Literatur, Links und Quellen:
http://www.cs.cmu.edu/~wjh/go/rules/Japanese.html
https://de.wikipedia.org/wiki/Go-Regeln
http://home.snafu.de/jasiek/rules.html
http://home.snafu.de/jasiek/j1989c.html
http://home.snafu.de/jasiek/j2003.html - http://home.snafu.de/jasiek/j2003com.html
https://govb.de/e107_files/public/1211027676_5_FT3069_regeln.pdf
http://denisfeldmann.fr/bestiary.htm

Andere Artikel über Japan lesen
Andere Länder-Essays lesen
Home